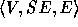 where V is a set of vertices, SE is a set of edges, and E is a
function from a subset of SE into
where V is a set of vertices, SE is a set of edges, and E is a
function from a subset of SE into  . It is assumed that
. It is assumed that
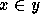 if and only if there exists an edge between x and y. He
defines the edges corresponding to the members of a set as
if and only if there exists an edge between x and y. He
defines the edges corresponding to the members of a set as
Zadrozny does not believe in a ``super theory'' of commonsense reasoning about sets, but rather in commonsense theories involving different aspects of sets. He thinks that these can be separately modeled in an existing set theory. In particular, he proposed a representation scheme based on Barwise's KPU for cardinality functions, hence distinguishing reasoning about well-orderings from reasoning about cardinalities and avoiding the box problem mentioned earlier (Zadrozny 1989).
Zadrozny interprets sets as directed graphs and does not assume the
FA. A graph in his conception is a triple 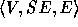 where V is a set of vertices, SE is a set of edges, and E is a
function from a subset of SE into
where V is a set of vertices, SE is a set of edges, and E is a
function from a subset of SE into 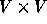 . It is assumed that
. It is assumed that
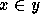 if and only if there exists an edge between x and y. He
defines the edges corresponding to the members of a set as
if and only if there exists an edge between x and y. He
defines the edges corresponding to the members of a set as
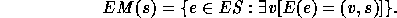
In classical set theory, the cardinality of a finite set s is a
one-to-one function from a natural number n onto a set, i.e., a
function from a number onto the nodes of the graph of the set.
However, Zadrozny defines the cardinality function as a one-to-one
order preserving mapping from the edges 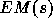 of a set s into the
numerals Nums (an entity of numerals which is linked with sets by
existence of a counting routine denoted by #, and which can take
values like 1,2,3,4, or 1,2,3, about-five, or 1,2,3,
many). The last element of the range of the function is the
cardinality. The representation of the four element set
of a set s into the
numerals Nums (an entity of numerals which is linked with sets by
existence of a counting routine denoted by #, and which can take
values like 1,2,3,4, or 1,2,3, about-five, or 1,2,3,
many). The last element of the range of the function is the
cardinality. The representation of the four element set 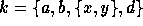 with three atoms and one two-atom set is shown in
Figure 17. The cardinality of the set is about-five,
i.e., the last element of Nums which is the range of the mapping
function from the edges of the set. (The cardinality might well be 4
if Nums was defined as 1,2,3,4.) Zadrozny then proves two important
theorems in which he shows that there exists a set x with n
elements which does not have a well ordering and there exists a well
ordering of type n, i.e., with n elements, the elements of which
do not form a set.
with three atoms and one two-atom set is shown in
Figure 17. The cardinality of the set is about-five,
i.e., the last element of Nums which is the range of the mapping
function from the edges of the set. (The cardinality might well be 4
if Nums was defined as 1,2,3,4.) Zadrozny then proves two important
theorems in which he shows that there exists a set x with n
elements which does not have a well ordering and there exists a well
ordering of type n, i.e., with n elements, the elements of which
do not form a set.
More recent work of Zadrozny treating different aspects of
computational mereology vis-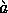 -vis set theory can be found in
(Zadrozny & Kim 1993).
-vis set theory can be found in
(Zadrozny & Kim 1993).
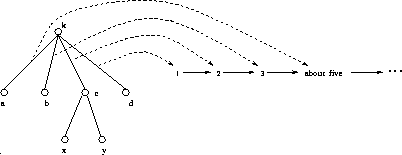
Figure 17: The one-to-one order preserving cardinality function of Zadrozny (adapted from (Zadrozny 1989))