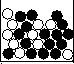
Figure 16: Balls with a finite cardinality but without a well ordering
There are other set-theoretical aspects like cardinality and well-ordering issues to be considered for a commonsense set theory. We have previously stated that classical set theory does provide a precise framework for mathematics. This assertion is arguable for commonsense reasoning. Minsky (1981), for example, had mentioned that the proof of the consistency of modern set theory indicates that it is inadequate for AI purposes and he criticized the popularity of formal logic in AI arguing that some important properties of logic, e.g., consistency and completeness, may not be desirable for knowledge representation. Indeed, as McCarthy (1977) pointed out, since there is no general agreement on the fundamental structure of the world, the need for precise representations might lead to the use of imprecise or inconsistent formalizations.
The following example illustrates this point (Zadrozny 1989). Imagine a box of 16 black and 10 white balls (Figure 16). We know that there are 26 balls in the box, or formally, the cardinality of the set of balls in the box is 26. After shaking the box, we would say that that the balls in the box are not ordered any more, or again formally, the set of the balls does not have a well-ordering. But this is not true in classical set theory, because a set with finite cardinality must have a well-ordering.

Figure 16: Balls with a finite cardinality but without a well ordering
Counting is an important activity to be mentioned at this point. While the formal principles of counting are precise enough for mathematics, we can observe that people also use other quantifiers like ``many'' or ``more than half'' for counting purposes in daily speech. For example, if asked about the number of balls in the box in Figure 16, one might have simply answered ``Many balls!'' So, at least in principle, different counting methods can be developed for commonsense reasoning. It is natural to expect, for example, that a system which can represent a statement like ``A group of kids are shouting'' should probably not answer questions such as ``Who is the first one?'' (Zadrozny 1989).
We also expect our theory to obey the parsimony principle. This is a
very natural expectation from a commonsense set theory. We have
observed that the proof of the existence of a simple fact like the
Cartesian product of two sets 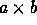 , required the use of the
Power Axiom in ZF. The set obtained in this manner just consists of
pairs formed of one element of the set a and one element of the set
b. To prove this, the strong Power Axiom should not be necessary.
We observe this in KPU set theory where the proof is obtained
(cf. Note 14) via definitions and simple axioms (Barwise 1975).
, required the use of the
Power Axiom in ZF. The set obtained in this manner just consists of
pairs formed of one element of the set a and one element of the set
b. To prove this, the strong Power Axiom should not be necessary.
We observe this in KPU set theory where the proof is obtained
(cf. Note 14) via definitions and simple axioms (Barwise 1975).