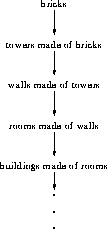
Figure 13: A hierarchical construction exemplifying the cumulative hierarchy (adapted from (Perlis 1988))
A theory proposed for commonsense reasoning should be examined from a variety of angles. We first begin with the general principles of set formation. The first choice that comes to mind is to allow urelements. This seems like the right thing to do because in a naive sense, a set is a collection of individuals satisfying a property. This is what exactly corresponds to the unrestricted Comprehension Axiom of Cantor. However, we have seen that this leads to Russell's Paradox in ZF. The problem arises when we use a set whose completion is not over yet in the formation of another set, or even in its own formation. Then we are led to the question when the collection of all individuals satisfying an expression can be considered an individual itself. Since we are talking about the individuals as entities formed out of previously formed entities, the notion of cumulative hierarchy immediately comes to mind.
The cumulative hierarchy is one of the most common construction mechanisms of our intuition and is supported by many existing theories, viz., ZF and KPU. It can be illustrated by the hierarchical construct in Figure 13, where we have bricks as our individuals, and make towers out of bricks, and then make walls out of towers, and so on. In the cumulative hierarchy, any set formed at some stage must be consisting of the urelements (if included in the theory) and the sets which have been formed at some previous stage (Shoenfield 1977) (but not necessarily at the very previous stage, as in Russell's Type Theory). This provides talking about collections of previously formed objects as a new object in a safe manner and prevents entities of very large size to be formed. Because a possible commonsense set theory also needs to be mathematically precise, it should take care of the question when a collection formed of previously formed sets will be considered as a set.

Figure 13: A hierarchical construction exemplifying the cumulative hierarchy (adapted from (Perlis 1988))
At this point, the problem of sets which can be members of themselves arises, since such sets are used in their own formation. Circularity is obviously a common means of commonsense knowledge representation. For example, non-profit organizations are sets of individuals and the set of all non-profit organizations is also a set; all these are expressible in the cumulative hierarchy. But what if the set of all non-profit organizations wants to be a member of itself, since it also is a non-profit organization? This is not an unexpected event (Figure 14) because this umbrella organization would probably benefit from having the status of a non-profit organization (e.g., tax exemption, etc.) (Perlis 1988).
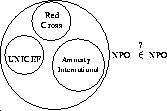
Figure 14: Can the set of non-profit-organizations be a member of itself?
Thus we conclude that a possible commonsense set theory should also allow circular sets to be expressed. This is an important issue in representation of meta-knowledge and is addressed in (Feferman 1984) and (Perlis 1985). In these references, a method which reifies (creates a syntactic term from a predicate expression) a well-formed formula into a name for the well-formed formula asserting that the name has strong relationship with the formula, is presented. In this way, any set of well-formed formulas are matched with a set of names of well-formed formulas, thereby allowing self-reference by the use of names. In (Feferman 1984), the urgent need for type-free (admitting instances of self-application) frameworks for semantics is especially emphasized. However, such formalizations which also capture the cumulative hierarchy principle are not very common. Among theories revised so far, Aczel's theory is the only one which allows circularity. By proposing his Anti-Foundation Axiom, Aczel overrode the FA of ZF which prohibits circular sets, but preserved the hierarchical nature of the original axiomatization.
As an application of such a theory, we see the Situation Theory (Barwise & Perry 1983). Situations are parts of the reality that can enter into relations with other parts. Their internal structures are sets of facts and hence they can be modeled by sets. There has been a considerable deal of work on this especially by Barwise himself (Barwise 1989a). He used his Admissible Set Theory (Barwise 1975) as the principal mathematical tool in the beginning. However, in the handling of circular situations, he was confronted with problems and then discovered that Aczel's theory could be a solution (Barwise 1989c). Circular situations are common in our daily life. For example consider the situation in which we utter the statement ``This is a very exciting situation.'' While we are referring to a situation, say s, by saying ``this situation,'' our utterance is also a part of that situation. As another example, one sometimes hears public announcements concluding with ``This announcement will not be repeated.'' If announcements are assumed to be situations, then this one surely contains itself.
Barwise defined the operation M (to model situations with sets) taking values in hypersets and satisfying (cf Note 12):
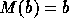 ,
,
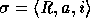 , then
, then 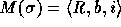 (which is called a state model), where b is a
function on the domain of a satisfying
(which is called a state model), where b is a
function on the domain of a satisfying 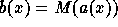 ,
,
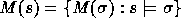 .
.
Using this operation, Barwise then proves some theorems, including the one which states that there is no largest situation (corresponding to the absence of a universal set in ZF).
We also see a treatment of self-reference in (Barwise & Etchemendy
1987), where the authors concentrate on the concept of truth. In this
study, two conceptions of truth are examined, primarily on the basis
of the notorious Liar Paradox (cf. Note 13). The authors make use of
Aczel's theory for this purpose. A statement like ``This sentence is
not expressible in English in ten words'' would be represented in
Aczel's theory as in Figure 15, where 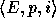 denotes that the proposition p has the property E if i =
1, and it does not have it if i = 0 (which is the case for the
figure if we take E to be the property of ``being expressible in
English in ten words'').
denotes that the proposition p has the property E if i =
1, and it does not have it if i = 0 (which is the case for the
figure if we take E to be the property of ``being expressible in
English in ten words'').
The model theory of common knowledge can also be studied using self-reference and situation theory (Barwise 1989d). This will be our next subject. The discussion on common knowledge will be followed by two discussions on membership and counting, respectively.
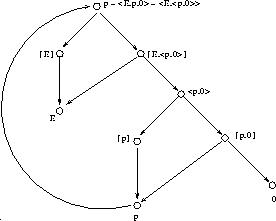
Figure 15: The picture of the statement ``This sentence is not expressible in English in ten words'' (adapted from (Barwise & Etchemendy 1987))