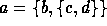 can be unambiguously depicted as in
Figure 6 in this representation (Aczel 1988), where an arrow
from a node x to a node y denotes the membership relation between
x and y (i.e.,
can be unambiguously depicted as in
Figure 6 in this representation (Aczel 1988), where an arrow
from a node x to a node y denotes the membership relation between
x and y (i.e., 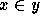 ).
).
It was Mirimanoff (1917) who first stated the fundamental difference
between well-founded and non-well-founded sets. He
called sets with no infinite descending membership sequence
well-founded and others non-well-founded. Non-well-founded sets have
been extensively studied through decades, but did not show up in
notable applications until Aczel. This is probably due to the fact
that the classical well-founded universe was a rather satisfying
domain for the practicing mathematician (``the mathematician in the
street'' (Barwise 1985)). Aczel's work on non-well-founded sets
evolved from his interest in modeling concurrent processes. He
adopted the graph representation for sets to use in his theory. A set
like 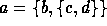 can be unambiguously depicted as in
Figure 6 in this representation (Aczel 1988), where an arrow
from a node x to a node y denotes the membership relation between
x and y (i.e.,
can be unambiguously depicted as in
Figure 6 in this representation (Aczel 1988), where an arrow
from a node x to a node y denotes the membership relation between
x and y (i.e., 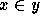 ).
).
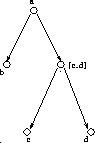
Figure 6: Representation of the set a in Aczel's conception
A set (pictured by a graph) is called well-founded if it has no
infinite paths or cycles, and non-well-founded otherwise. Aczel's
Anti-Foundation Axiom, AFA, states that every graph,
well-founded or not, pictures a unique set. Removing the Axiom of
Foundation (FA) from the ZFC and adding the AFA results in the
Hyperset Theory. (ZFC without FA is denoted as ZFC .) What is
advantageous with the new theory is that since graphs of arbitrary
form are allowed, including the ones containing proper cycles, one can
represent self-referring sets. For example, the graph in
Figure 7 is the picture of the unique set
.) What is
advantageous with the new theory is that since graphs of arbitrary
form are allowed, including the ones containing proper cycles, one can
represent self-referring sets. For example, the graph in
Figure 7 is the picture of the unique set 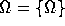 .
.
The picture of a set can be unfolded into a tree picture of
the same set. The tree whose nodes are the finite paths of the apg
(cf. Note 11) which start from the point of the apg, whose edges are
pairs of paths 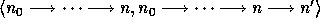 , and whose root is the path
, and whose root is the path 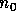 of length one is called the
unfolding of that apg. The unfolding of an apg always
pictures any set pictured by that apg. Unfolding the apg in
Figure 7 results in an infinite tree, analogous to
of length one is called the
unfolding of that apg. The unfolding of an apg always
pictures any set pictured by that apg. Unfolding the apg in
Figure 7 results in an infinite tree, analogous to
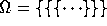 .
.
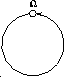
Figure 7: The picture of the circular set 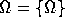
According to Aczel's conception, for two sets to be different, there
should be a genuine structural difference between them. (Therefore
all the three graphs in Figure 8 depict the unique
non-well-founded set 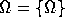 .)
.)
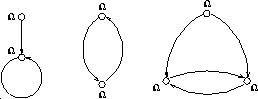
Figure 8: Other graphs depicting 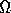
Aczel develops his own extensionality concept by introducing the
notion of bisimulation. A bisimulation between two apg's,
 with point
with point  and
and 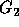 with point
with point 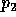 , is a relation
, is a relation 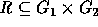 satisfying the following conditions:
satisfying the following conditions:
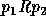
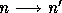 of
of  , there exists
an edge
, there exists
an edge 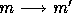 of
of  such that
such that 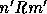
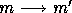 of
of 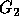 , there exists
an edge
, there exists
an edge 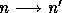 of
of 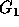 such that
such that 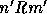
Two apg's 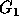 and
and 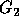 are said to be bisimilar, if a
bisimulation exists between them; this means that they picture the
same sets. It can be concluded that a set is completely determined by
any graph which pictures it.
are said to be bisimilar, if a
bisimulation exists between them; this means that they picture the
same sets. It can be concluded that a set is completely determined by
any graph which pictures it.
The uniqueness property of AFA leads to an intriguing concept of
extensionality for hypersets. The classical extensionality paradigm,
that sets are equal if and only if they have the same members, works
fine with well-founded sets. However, this is not of use in deciding
the equality of say, 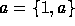 and
and 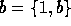 because it just
asserts that a=b if and only if a=b, a triviality (Barwise &
Etchemendy 1987). However, in the universe of hypersets, a is
indeed equal to b since they are depicted by the same graph. To see
this, consider a graph G and a decoration D assigning a to a
node x of G, i.e.,
because it just
asserts that a=b if and only if a=b, a triviality (Barwise &
Etchemendy 1987). However, in the universe of hypersets, a is
indeed equal to b since they are depicted by the same graph. To see
this, consider a graph G and a decoration D assigning a to a
node x of G, i.e., 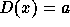 . Now consider the decoration
. Now consider the decoration 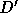 exactly the same as D except that
exactly the same as D except that 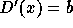 .
. 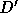 must also be a
decoration for G. But by the uniqueness property of AFA,
must also be a
decoration for G. But by the uniqueness property of AFA, 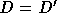 , so
, so
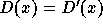 , and therefore a=b.
, and therefore a=b.
The AFA universe can be depicted as in Figure 9, extending around the well-founded universe, because it includes the non-well-founded sets which are not covered by the latter.

Figure 9: AFA universe extending around the well-founded universe (adapted from (Barwise & Etchemendy 1987))