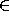Admissible sets are formalized in a first order set theory
called Kripke-Platek (KP) (Kripke 1964). Barwise weakened KP
to a new theory KPU by readmitting the urelements (Barwise
1975). Urelements are the objects (or individuals) with no elements,
i.e., they can occur on the left of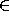 
, but not on the right. They
are not considered in ZF because ZF is strong enough to live without
them. But since KPU is a weak version of KP, Barwise decided to
include them.
KPU is formulated in a first order language L with equality and with
the membership symbol added. It has six axioms. The axioms of
Extensionality and Foundation are about the basic nature of
sets. The axioms Pair, Union, and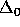 
-
Separation (cf. Note 9) treat the principles of set construction.
These five axioms can be taken as corresponding to ZF axioms of the
same interpretation. The important axiom of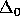 
-
Collection assures that there are enough stages in the
(hierarchical) construction process.
The universe of admissible sets over an arbitrary collection M of urelements is defined recursively:
,
,
,
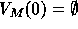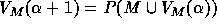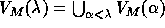if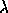 
is a limit ordinal,
.
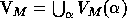where P is the power operation, and 
and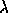 
are
ordinals. This universe can be depicted as in Figure 3.
It should be noticed that the KPU universe is like the ZF universe
(excluding the existence of urelements), since it supports the same
idea of cumulative hierarchy (Barwise 1977).
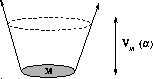
Figure 3: The universe of admissible sets (adapted from (Barwise 1975))
If M is a structure (cf. Note 10) for L, then an admissible
set over M is a model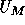 
of KPU of the form 
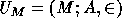, where A is a nonempty set of non-urelements and 
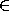is
defined in 
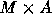. Such a typical admissible set over M can
be depicted as in Figure 4. A pure admissible
set is an admissible set with no urelements, i.e., it is a model of
KP. Such a set can be depicted as in Figure 5.
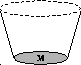
Figure 4: A typical admissible set (adapted from (Barwise 1975))
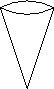
Figure 5: A pure admissible set (adapted from (Barwise 1975))
KPU is an elegant theory which supports the concept of cumulative hierarchy and respects the principle of parsimony. (The latter claim will be proved in the sequel.) But it still cannot deal with self-reference because of its hierarchical nature.