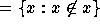The new axiomatizations took a common step for overcoming the
deficiencies of the naive approach by introducing classes, a
membership-eligible entity corresponding a given condition. NBG,
which was proposed by von Neumann (1925) and later revised and
simplified by Bernays (1937) and Gödel (1940), was the most
popular of these. In NBG, there are three primitive notions: set,
class, and membership. Classes are considered as totalities
corresponding to some, but not necessarily all, properties. The
classical paradoxes are avoided by recognizing two types of classes:
sets and proper classes. A class is a set if it is a member of some
class. Otherwise, it is a proper class. Russell's Paradox is avoided
by showing that the class Y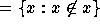 
is a proper class,
not a set. V is also considered as a proper class. The axioms of NBG
are simply chosen with respect to the limitation of size constraint.
Strengthening NBG by replacing the axioms of class existence with an axiom scheme, a new theory called Morse-Kelley (MK) is obtained (Morse 1965). MK is suitable if one is not interested in the subtleties of set theory. But its strength risks its consistency (Mendelson 1987).
Ackermann (1956) also proposed an axiomatization again employing classes, but in which the central objects are sets. The main point of this axiomatization is that its axioms retain only the weakest consequences of the limitation of size constraint, i.e., a member of a set and a subclass of a set are sets.
Other approaches against the deficiencies of the naive approach
alternatively played with its language and are generally called
type-theoretical approaches. Russell and Whitehead's Theory
of Types is the earliest and most popular of these (Whitehead &
Russell 1910). In this theory, a hierarchy of types is established to
forbid circularity and hence avoid paradoxes. For this purpose, the
universe is divided into types, starting with a collection M of
individuals. The elements of M are of type 0. Sets whose
members are of type 0 are said to be of type 1, sets whose elements
are of type 1 are said to be of type 2, and so on. The membership
relation is defined between sets of different types, e.g.,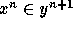 
. Therefore, 
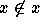is not even a valid formula in
this theory and Russell's Paradox is avoided.
Similar to the Theory of Types is Quine's New Foundations (NF)
which he invented to overcome some unpleasant aspects of the former
(Quine 1937). NF uses only one kind of variable and a binary
predicate letter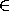 
for membership. A notion called
stratification is introduced to maintain the hierarchy of types
(cf. Note 2). In NF, Russell's Paradox is avoided as in the Theory of
Types, since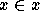 
is not stratified.