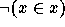 in the
language of first-order logic. (
in the
language of first-order logic. (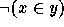 will be denoted as
will be denoted as 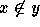 from now on.)
from now on.)
G. Cantor's work on the theory of infinite series and related topics should be considered as the foundation of the research in set theory. In Cantor's conception, a set, or aggregate, is a collection into a whole of definite, distinct objects of our perception or our thought, called the elements of the set (Cantor 1883). This property of definiteness implies that given a set and an object, it is possible to determine if the object is a member of that set; in other words, a set is completely determined by its members.
In the earlier stages of his research, Cantor did not work from axioms (Suppes 1972). However, all of his theorems can be derived from three axioms: Extensionality which states that two sets are identical if they have the same members, Abstraction which states that for any given property there is a set whose members are just those entities having that property, and Choice which states that if b is a set, all of whose elements are non-empty sets no two of which have any elements in common, then there is a set c which has precisely one element in common with each element of b.
The theory was soon threatened by the introduction of some paradoxes
which led to its evolution. In 1902, Russell found a contradiction in
Frege's foundational system (Frege 1893) which was developed on
Cantor's naive set conception (van Heijenhoort 1967). Frege's reaction
to this can be found in the appendix to the second volume of his
famous Grundgesetze der Arithmetik: ``Hardly anything more
unfortunate can befall a scientific writer than to have one of the
foundations of his edifice shaken after the work is finished. This was
the position I was placed in by a letter of Mr. Bertrand Russell.''
This contradiction could be derived from the Axiom of Abstraction
(which was named Axiom V in Frege's system) by considering ``the set
of all things which have the property of not being members of
themselves.'' This property can be denoted as 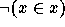 in the
language of first-order logic. (
in the
language of first-order logic. (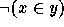 will be denoted as
will be denoted as 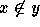 from now on.)
from now on.)
The Axiom of Abstraction can be formulated as

where 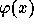 is a formula in which y is free. In the case of
Russell's Paradox
is a formula in which y is free. In the case of
Russell's Paradox 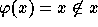 and we have:
and we have: 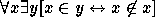 . Substituting y
for x, we reach
. Substituting y
for x, we reach 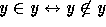 . The
problematic thing here is the set x with the property
. The
problematic thing here is the set x with the property 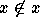 .
.
Another antinomy occurred with the conception of the ``set of all
sets,'' V 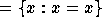 . The well-known Cantor's Theorem states
that the power set (set of all subsets) of V has a greater cardinality
than V itself. This is obviously paradoxical since V by definition is
the most inclusive set. This is the so-called Cantor's Paradox (Cantor
1932) and led to discussions on the sizes of comprehensible sets.
Strictly speaking, it was Frege's foundational system that was
overthrown by Russell`s Paradox, not Cantor's naive set theory. The
latter came to grief precisely because of the preceding ``limitation
of size'' constraint. Later, von Neumann would clarify this problem
of size by stating that (Goldblatt 1984) ``Some predicates have
extensions that are too large to be successfully encompassed as a
whole and treated as a mathematical object.''
. The well-known Cantor's Theorem states
that the power set (set of all subsets) of V has a greater cardinality
than V itself. This is obviously paradoxical since V by definition is
the most inclusive set. This is the so-called Cantor's Paradox (Cantor
1932) and led to discussions on the sizes of comprehensible sets.
Strictly speaking, it was Frege's foundational system that was
overthrown by Russell`s Paradox, not Cantor's naive set theory. The
latter came to grief precisely because of the preceding ``limitation
of size'' constraint. Later, von Neumann would clarify this problem
of size by stating that (Goldblatt 1984) ``Some predicates have
extensions that are too large to be successfully encompassed as a
whole and treated as a mathematical object.''
Such paradoxes shook the theory to its foundations and were instrumental in new axiomatizations of the set theory or in alternate approaches. However, it is believed that axiomatic set theory would still have evolved in the absence of paradoxes because of the continuous search for foundational principles. Axiomatization of a theory is important since it provides a concise formulation of the principles of the theory and allows fundamental notions like completeness and consistency to be discussed in a precise way; these would be formulated in an imprecise manner (e.g., in natural language) otherwise.