


Next: CONCLUSION
Up: Some Interesting Attempts
Previous: Protosets of Mislove
Barwise (1989b) attempted to propose a set theory, Situated Set
Theory, not just for use in AI, but for general use. He mentioned
the problems caused by the common view of set theory with a universal
set V, but at the same time trying to treat this universe as an
extensional whole, looking from outside (which he names ``unsituated
set theory''). His proposal is a hierarchy of universes 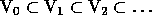 which allows
for a universe of a lower level to be considered as an object of a
universe of a higher level. He leaves the axioms which these
universes have to satisfy to one's conception of set, be it cumulative
or circular. There are no paradoxes in this view since there is
always a larger universe one can step back and work in. Therefore,
the notions of ``set,'' ``proper class,'' and the set-theoretic
notions ``ordinal,'' ``cardinal'' are all context sensitive, depending
on the universe one is currently working in. This proposal supports
the Reflection Principle which states that for any given
description of the sets of all sets V, there will always be a partial
universe satisfying that description.
which allows
for a universe of a lower level to be considered as an object of a
universe of a higher level. He leaves the axioms which these
universes have to satisfy to one's conception of set, be it cumulative
or circular. There are no paradoxes in this view since there is
always a larger universe one can step back and work in. Therefore,
the notions of ``set,'' ``proper class,'' and the set-theoretic
notions ``ordinal,'' ``cardinal'' are all context sensitive, depending
on the universe one is currently working in. This proposal supports
the Reflection Principle which states that for any given
description of the sets of all sets V, there will always be a partial
universe satisfying that description.
Barwise (1989c) also studied the modeling of partial information and
again exploited Hyperset Theory for this purpose. For this purpose,
he used the objects of the universe 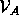 of hypersets over a
set A of atoms to model non-parametric objects, i.e., objects with
complete information and the set X of indeterminates to
represent parametric objects, i.e., objects with partial
information. (The universe of hypersets on
of hypersets over a
set A of atoms to model non-parametric objects, i.e., objects with
complete information and the set X of indeterminates to
represent parametric objects, i.e., objects with partial
information. (The universe of hypersets on 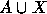 is denoted as
is denoted as
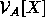 , analogous to the adjunction of indeterminates in
algebra.)
, analogous to the adjunction of indeterminates in
algebra.)
For any object 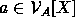 , Barwise calls the set
, Barwise calls the set
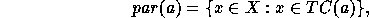
where 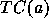 denotes the transitive closure of a, the
set of parameters of a. If
denotes the transitive closure of a, the
set of parameters of a. If 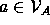 , then
, then 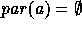 since a does not have any parameters. Barwise then
defines an anchor as a function f with
since a does not have any parameters. Barwise then
defines an anchor as a function f with 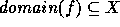 and
and 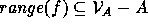 which assigns sets to
indeterminates. For any
which assigns sets to
indeterminates. For any 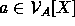 and anchor f,
and anchor f,
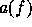 is the object obtained by replacing each indeterminate
is the object obtained by replacing each indeterminate 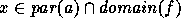 by the set
by the set 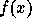 in a. This is accomplished
by solving the resulting equations by the Solution Lemma.
in a. This is accomplished
by solving the resulting equations by the Solution Lemma.
Parametric anchors can also be defined as functions from a subset of
X into 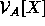 to assign parametric objects, not just
sets, to indeterminates. For example, if
to assign parametric objects, not just
sets, to indeterminates. For example, if 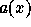 is a parametric
object representing partial information about some non-parametric
object
is a parametric
object representing partial information about some non-parametric
object 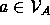 and if one does not know the value to
which x is to be anchored, but knows that it is of the form
and if one does not know the value to
which x is to be anchored, but knows that it is of the form 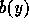 (another parametric object), then anchoring x to
(another parametric object), then anchoring x to 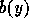 results in
the object
results in
the object 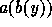 which does not give the ultimate object perhaps,
but is at least more informative about its structure.
which does not give the ultimate object perhaps,
but is at least more informative about its structure.



Next: CONCLUSION
Up: Some Interesting Attempts
Previous: Protosets of Mislove
Varol Akman
Sat Jan 13 15:54:04 EET 1996
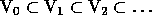 which allows
for a universe of a lower level to be considered as an object of a
universe of a higher level. He leaves the axioms which these
universes have to satisfy to one's conception of set, be it cumulative
or circular. There are no paradoxes in this view since there is
always a larger universe one can step back and work in. Therefore,
the notions of ``set,'' ``proper class,'' and the set-theoretic
notions ``ordinal,'' ``cardinal'' are all context sensitive, depending
on the universe one is currently working in. This proposal supports
the Reflection Principle which states that for any given
description of the sets of all sets V, there will always be a partial
universe satisfying that description.
which allows
for a universe of a lower level to be considered as an object of a
universe of a higher level. He leaves the axioms which these
universes have to satisfy to one's conception of set, be it cumulative
or circular. There are no paradoxes in this view since there is
always a larger universe one can step back and work in. Therefore,
the notions of ``set,'' ``proper class,'' and the set-theoretic
notions ``ordinal,'' ``cardinal'' are all context sensitive, depending
on the universe one is currently working in. This proposal supports
the Reflection Principle which states that for any given
description of the sets of all sets V, there will always be a partial
universe satisfying that description.
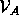 of hypersets over a
set A of atoms to model non-parametric objects, i.e., objects with
complete information and the set X of indeterminates to
represent parametric objects, i.e., objects with partial
information. (The universe of hypersets on
of hypersets over a
set A of atoms to model non-parametric objects, i.e., objects with
complete information and the set X of indeterminates to
represent parametric objects, i.e., objects with partial
information. (The universe of hypersets on 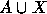 is denoted as
is denoted as
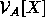 , analogous to the adjunction of indeterminates in
algebra.)
, analogous to the adjunction of indeterminates in
algebra.)
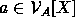 , Barwise calls the set
, Barwise calls the set
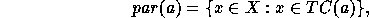
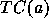 denotes the transitive closure of a, the
set of parameters of a. If
denotes the transitive closure of a, the
set of parameters of a. If 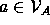 , then
, then 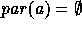 since a does not have any parameters. Barwise then
defines an anchor as a function f with
since a does not have any parameters. Barwise then
defines an anchor as a function f with 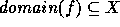 and
and 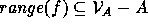 which assigns sets to
indeterminates. For any
which assigns sets to
indeterminates. For any 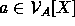 and anchor f,
and anchor f,
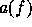 is the object obtained by replacing each indeterminate
is the object obtained by replacing each indeterminate 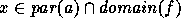 by the set
by the set 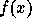 in a. This is accomplished
by solving the resulting equations by the Solution Lemma.
in a. This is accomplished
by solving the resulting equations by the Solution Lemma.
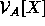 to assign parametric objects, not just
sets, to indeterminates. For example, if
to assign parametric objects, not just
sets, to indeterminates. For example, if 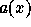 is a parametric
object representing partial information about some non-parametric
object
is a parametric
object representing partial information about some non-parametric
object 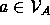 and if one does not know the value to
which x is to be anchored, but knows that it is of the form
and if one does not know the value to
which x is to be anchored, but knows that it is of the form 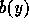 (another parametric object), then anchoring x to
(another parametric object), then anchoring x to 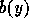 results in
the object
results in
the object 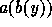 which does not give the ultimate object perhaps,
but is at least more informative about its structure.
which does not give the ultimate object perhaps,
but is at least more informative about its structure.