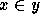 , the integer assigned to y is equal to the integer assigned
to x + 1. For example,
, the integer assigned to y is equal to the integer assigned
to x + 1. For example, 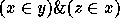 is stratified as
is stratified as
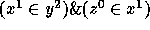 .
.
1. Note, on the other hand, that another great mathematician of this century, R. Thom, has said in 1971: ``The old hope of Bourbaki, to see mathematical structures arise naturally from a hierarchy of sets, from their subsets, and from their combination, is doubtless, only an illusion'' (Goldblatt 1984).
2. A well-formed formula w is said to be stratified
if integers are assigned to the variables of w such that all
occurrences of the same free variable are assigned the same integer,
all bound occurrences of a variable that are bound by the same
quantifier are assigned the same integer, and for every subformula 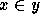 , the integer assigned to y is equal to the integer assigned
to x + 1. For example,
, the integer assigned to y is equal to the integer assigned
to x + 1. For example, 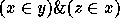 is stratified as
is stratified as
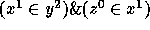 .
.
3. In every subset of the set of natural numbers, ordered according
to increasing magnitude of its elements, there is a first element.
This also holds for arbitrary ordered sets as follows. A binary
relation < over a set a is a partial ordering of a if
(i) 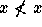 for any
for any 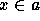 , and (ii) if x < y and y < z,
then x < z. (a is called a partially ordered set.) A
partial ordering < of a is a linear ordering if x < y,
or x = y, or y < x, for all
, and (ii) if x < y and y < z,
then x < z. (a is called a partially ordered set.) A
partial ordering < of a is a linear ordering if x < y,
or x = y, or y < x, for all 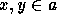 . If a is a partially
ordered set and b is a nonempty subset of a, and
. If a is a partially
ordered set and b is a nonempty subset of a, and 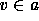 , then
v is called the least element of b if
, then
v is called the least element of b if 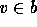 and
and
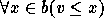 , and w is called a minimal
element of b if
, and w is called a minimal
element of b if 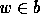 and
and 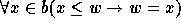 .
.
4. A theory T (any set of formulas closed under implication,
i.e., for any 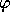 , if
, if 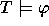 , then
, then 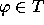 )
is finitely axiomatizable if and only if there is a finite
)
is finitely axiomatizable if and only if there is a finite 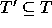 such that for every
such that for every 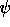 in T,
in T, 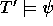 .
.
5. Cantor (1883) stated that two sets are equipollent, or have the same power, if and only if they can be put into one-to-one correspondence. The axiom for cardinal numbers states that two sets have the same cardinality if they are equipollent, denoted by |x| = |y|. m is a cardinal number if and only if there is a set a such that |a| = m.
6. A linear ordering < of a set a is a well-ordering if
every nonempty subset of a has a least element. Informally, an
ordered set is said to be well-ordered if the set itself, and
all its nonempty subsets have a first element under the order
prescribed for its elements by that set. An ordinal number stands for
an order type which is represented by well-ordered sets. First, call
a set a transitive if 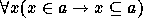 . Then, a set is an ordinal number (or ordinal) if it is
transitive and well-ordered by
. Then, a set is an ordinal number (or ordinal) if it is
transitive and well-ordered by 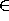 . It should be noted that in case
of finite sets, the notions of cardinal number and ordinal number are
the same. The class of all ordinal numbers is denoted by Ord. The
relationship < between two ordinals
. It should be noted that in case
of finite sets, the notions of cardinal number and ordinal number are
the same. The class of all ordinal numbers is denoted by Ord. The
relationship < between two ordinals  and
and 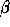 ,
, 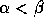 , is defined if and only if
, is defined if and only if 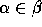 . If
. If 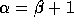 , then
, then  is called a successor ordinal; else
it is a limit ordinal. The Axiom of Infinity guarantees the
existence of limit ordinals other than 0. In fact,
is called a successor ordinal; else
it is a limit ordinal. The Axiom of Infinity guarantees the
existence of limit ordinals other than 0. In fact, 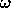 , the set
of natural numbers, is the next limit ordinal.
, the set
of natural numbers, is the next limit ordinal.
7. A group 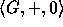 (where G is a nonempty set, + is a function mapping
(where G is a nonempty set, + is a function mapping 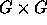 into G, and
into G, and 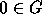 ) satisfies the following axioms:
) satisfies the following axioms:
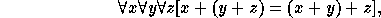


An Abelian group is a group G satisfying:
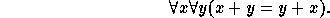
An Abelian group is divisible if
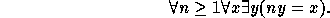
It should be noted that this axiom is not first-order since there is a quantification over the set of positive integers. Hence, a divisible Abelian group is not finitely axiomatizable in first-order logic. An Abelian group is torsion if

The last remark regarding axiomatizability applies to torsion groups, too.
8. We have to prove the theorem
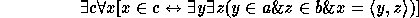
to show that the Cartesian product set exists. The main point of the
proof is that if 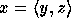 , and if
, and if 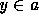 and
and 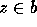 , then
, then 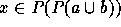 . Then, by the Axiom of
Separation,
. Then, by the Axiom of
Separation,
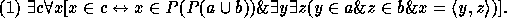
The theorem to be proved is equivalent to (1) without the
statement 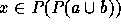 . Then we must show that the
equivalence in (1) still holds when that statement is
eliminated. Given (1), it follows that
. Then we must show that the
equivalence in (1) still holds when that statement is
eliminated. Given (1), it follows that

implies
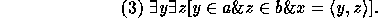
To prove the converse implication, we must show that (3)
implies 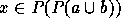 , since it is obvious by (1)
that (3) implies (2). By (3) and the
definition of ordered pairs
, since it is obvious by (1)
that (3) implies (2). By (3) and the
definition of ordered pairs 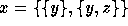 , and by the
hypotheses
, and by the
hypotheses 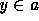 and
and 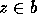 , we have:
, we have:
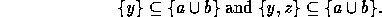
Then by the following theorem (which can be proved by the Power Axiom):
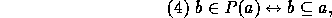
we conclude:
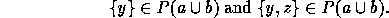
Thus, 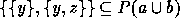 , i.e.,
, i.e., 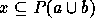 , and again by (4), we have
, and again by (4), we have 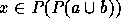 .
.
9. The collection of 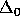 formulas of a
language L is the smallest collection
formulas of a
language L is the smallest collection 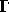 containing the atomic
formulas of L and inductively defined as:
containing the atomic
formulas of L and inductively defined as:
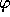 is in
is in 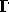 , then
, then 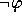 is also in
is also in 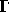 .
.
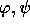 are in
are in 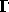 , then
, then 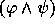 and
and 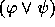 are also in
are also in 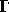 .
.
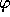 is in
is in 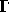 , then
, then 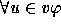 and
and 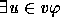 are also in
are also in 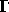 for all
variables u and v.
for all
variables u and v.
10. A structure for a first-order language L is a pair
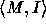 , where M is a nonempty set called the
domain of the structure and I is an interpretation
function assigning functions and predicates over M to the symbols
in L (Mendelson 1987).
, where M is a nonempty set called the
domain of the structure and I is an interpretation
function assigning functions and predicates over M to the symbols
in L (Mendelson 1987).
11. Aczel uses tagged graphs to represent sets, i.e.,
each childless node in the graph is tagged by an atom or
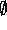 . A pointed graph is a tagged graph with a
specific node
. A pointed graph is a tagged graph with a
specific node 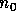 called its point. A pointed graph is
accessible (denoted as apg) if for every node n there is a path
called its point. A pointed graph is
accessible (denoted as apg) if for every node n there is a path
 . A decoration of a graph is a function
. A decoration of a graph is a function 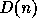 for each
node n, defined as:
for each
node n, defined as:
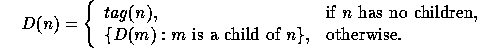
A picture of a set is an apg which has a decoration in which the set is assigned to the point.
12. A state of affair (a.k.a. infon) 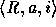 is a triple where R is an n-ary relation, a is an
appropriate assignment of objects, and i is the polarity, 1 if there
is at least one instance of R holding of a, and 0 otherwise. By a
state of affair, a state that affairs may or may not be in is meant.
When i=1, that state of affair is called a fact and the
polarity is usually omitted. For example, the state of affair
is a triple where R is an n-ary relation, a is an
appropriate assignment of objects, and i is the polarity, 1 if there
is at least one instance of R holding of a, and 0 otherwise. By a
state of affair, a state that affairs may or may not be in is meant.
When i=1, that state of affair is called a fact and the
polarity is usually omitted. For example, the state of affair
 sleeping,Tom,garden
sleeping,Tom,garden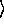 is a fact if Tom is indeed
sleeping in the garden.
is a fact if Tom is indeed
sleeping in the garden.
13. The word paradox refers to any statement which is contrary to common sense and intuition. The Liar Paradox (also known as the Epimenides Paradox) is one of the most famous paradoxes which disturbed philosophers, mathematicians, and linguists throughout history. According to this paradox, Epimenides, the Cretan, said ``All Cretans are liars.'' Now this statement cannot be true since this would make Epimenides a liar, leading to the falsity of his statement. The statement cannot be false either, since this would imply that Cretans are not liars, hence what Epimenides says should be true, leading to a contradiction.
14. The predicate of a,b,u, which is defined as ``u is an
ordered pair 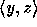 with
with 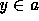 and
and 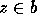 '' in
KPU, is
'' in
KPU, is 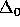 . Hence,
. Hence, 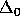 -Separation can be used once it
is known that there exists a set c with
-Separation can be used once it
is known that there exists a set c with 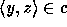 for all
for all 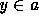 and
and 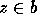 . This follows from
. This follows from
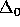 -Collection as follows. Given
-Collection as follows. Given 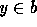 , there exists a set
, there exists a set
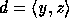 . So, by
. So, by 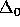 -Collection, there exists
a set
-Collection, there exists
a set 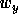 such that
such that 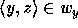 for all
for all 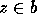 . Applying
. Applying 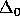 -Collection again, we have:
-Collection again, we have:
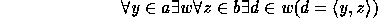
so there is a 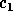 such that for all
such that for all 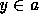 ,
, 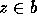 ,
, 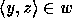 for some
for some 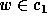 . Thus, if
. Thus, if 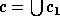 ,
then
,
then 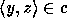 for all
for all 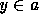 and
and 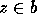 .
.
15. Circumscription is a tool to jump to certain conclusions. The
main point of circumscription is that the objects that can be shown to
have a certain property 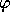 by reasoning from certain facts are
all the objects that satisfy
by reasoning from certain facts are
all the objects that satisfy 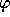 . Thus one
circumscribes the set of objects.
. Thus one
circumscribes the set of objects.
16. The  is the notation for first writing all
is the notation for first writing all  symbols in terms of
symbols in terms of 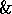 and
and  , then passing negations in
, then passing negations in
 through to predicate letters, and finally replacing each
occurrence of a subformula
through to predicate letters, and finally replacing each
occurrence of a subformula 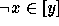 in the result by
in the result by 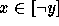 .
.
17. The transitive closure of a set, denoted by 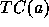 , is
defined by recursion as follows:
, is
defined by recursion as follows:
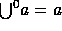 ,
,
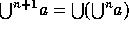 ,
,
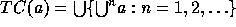 .
.
Hence, 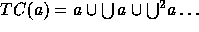 For any
infinite cardinal m, the set
For any
infinite cardinal m, the set 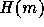 is defined as
is defined as 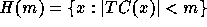 . The elements of
. The elements of 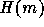 are said to be
hereditarily of cardinality less than m.
are said to be
hereditarily of cardinality less than m. 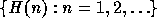 is the set of hereditarily finite sets. Hence,
every element of a hereditary set is a hereditary set (Kunen 1980).
is the set of hereditarily finite sets. Hence,
every element of a hereditary set is a hereditary set (Kunen 1980).